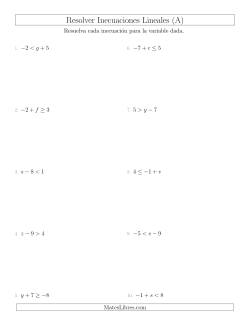Bienvenido a la página de Algebra de MatesLibres.com, donde las incógnitas son comunes y las variables son la norma. Estas hojas de ejercicios están destinadas principalmente a los estudiantes de secundaria, pero hemos tocado también algunos temas de preuniversitario.
Esta página comienza con algunas hojas de ejercicios de completar números en blanco, para los estudiantes más jóvenes. Saltamos entonces directo hacia el álgebra, ayudando a los estudiantes a reconocer y comprender su lenguaje básico. El resto de la página cubre algunos de los temas principales que encontrarán en las unidades de álgebra. Recuerde que al enseñarle álgebra a sus estudiantes, está ayudando a crear los genios financieros, los ingenieros y los científicos del futuro, que resolverán todos los problemas de nuestro mundo.
Hojas de Ejercicios de álgebra más populares esta semana




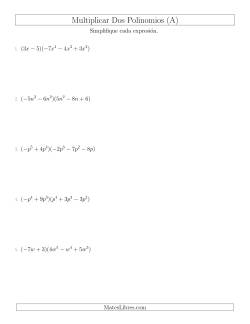
El álgebra es mucho más interesante cuando los problemas son más reales. Resolver ecuaciones lineales es mucho más interesante con una balanza de dos platos, algunas bolsas misteriosas y un montón de caramelos. Muchos profesores emplean losas de álgebra para ayudar a los estudiantes a comprender una variedad de temas sobre álgebra. Y no hay nada como un sistema de ejes coordenados para solucionar sistemas de ecuaciones lineales.
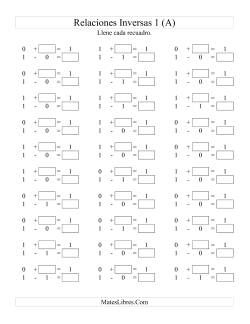
Relaciones Inversas
Los ejercicios de relaciones inversas cubren una habilidad de pre-álgebra destinada a que los estudiantes comprendan la relación entre la multiplicación y la división, y la de la suma con la resta.
Relaciones Inversas con Un Espacio en Blanco

Relaciones Inversas con Dos Espacios en Blanco
Números en Blanco
Las hojas de ejercicios de números en blanco vienen en tres versiones. La más simple incluye sólo espacios en blanco; la siguiente usa símbolos para las incógnitas; y la tercera incluye variables para las incógnitas. Las versión con espacios en blanco es una buena manera para inculcar algún pensamiento algebraico en los estudiantes más jóvenes.
Operaciones con Espacios en Blanco

Operaciones con Símbolos

Operaciones con Variables

Igualdades con Sumas en Ambos lados, donde las Incógnitas son Símbolos

Expresiones Algebraicas
Propiedad Distributiva

Evaluar Expresiones Algebraicas

Reglas de Exponentes
Como dice el título, estos ejercicios incluyen preguntas básicas sobre las reglas de los exponentes. Cada pregunta sólo tiene dos exponentes; no se incluyen términos complicados ni temas pra estudiantes más avanzados. Por ejemplo, 42 = (22)2 = 24, pero estos ejercicios lo dejan en 42, para que los estudiantes enfocarse en multiplicar y dividir exponentes más o menos aislados.
Práctica con Reglas Básicas de Exponentes
Expresiones y Ecuaciones Lineales
Ejercicios de ecuaciones lineales que incluyen simplificar, graficar, evaluar y resolver sistemas de ecuaciones lineales.
Aquí hay un buen material de impresión para traducir frases en español a expresiones algebraicas. Recuerde siempre que se trata de un documento de otro sitio.
Simplificar Expresiones Lineales (Combinar Términos Semejantes)

Sumar, Restar y Simplificar Expresiones Lineales
Reescribir Ecuaciones Lineales

Determinar ecuaciones lineales a partir de pendientes, interceptos y , y puntos

Gráficos de Ecuaciones Lineales
Puede que lo haya intrigado nuestro comentario sobre resolver ecuaciones lineales con caramelos. Así es como se se logra: Idealmente, uno querría bolsas opacas sin masa, pero como eso no es posible (la parte de la masa), hay una pequeña condición que incluso ayudará a los estudiantes a comprender mejor las ecuaciones. Las bolsas que se empleen deben estar balanceadas en el otro platillo con bolsas vacías.
Probablemente la mejor manera de ilustrar esto sea con un ejemplo. Usemos 3x + 2 = 14. Puede que reconozca la x como la incógnita que es en realidad el número de caramelos que ponemos en cada bolsa opaca. El 3 de 3x significa que necesitaremos tres bolsas. Es mejor llenar las bolsas con la cantidad necesaria de caramelos sin que los estudiantes lo vean, para que tengan que resolver la ecuación realmente.
En un lado de la balanza de dos platos, coloque las tres bolsas con x caramelos en cada una, y dos caramelos sueltos para representar el + 2 de la ecuación. Del otro lado de la balanza, coloque 14 caramelos y tres bolsas vacías que, como se dijo antes, sirven para "balancear" la ecuación correctamente. Ahora viene la parte divertida... si los estudiantes quitan los dos caramelos sueltos de un lado de la ecuación, las cosas pierden el balance, asíque necesitan quitar dos caramelos del otro lado también para emparejar. Comerse los caramelos es opcional. El objetivo es aislar las bolsas de un lado de la balanza sin ningún caramelo suelto a la vez que se balancea la ecación.
El último paso es dividir los caramelos sueltos en tantos grupos como hay bolsas del otro lado de la balanza. Esto les dará una buena idea de cuántos caramelos hay en cada bolsa. Si no, cómanse algunos e inténtenlo de nuevo. Estamos conscientes de que esto no funcionará para todas las ecuaciones lineales, ya que es difícil encontrar caramelos negativos, pero es otra estrategia que puede emplear para enseñar álgebra.
Aunque a primera vista puedan parecerlo, las ecuaciones del tipo a/x no son lineales, sino que pertenecen a otra clase de ecuaciones. Sin embargo, es bueno trabajar con ellas para introducir el concepto de soluciones válidas y no válidas de una ecuación (lo que más adelante se llamará dominio de una función). En este caso, las soluciones no válidas de las ecuaciones del tipo a/x son las que hacen que el denominador sea igual a 0.
Resolver Ecuaciones Lineales

Sistemas Lineales
Resolver Sistemas Lineales

Resolver Sistemas Lineales Graficando
Ecuaciones y Expresiones Cuadráticas
Los ejercicios de factorización siguientes proporcionan muchas preguntas de práctica pra que los estudiantes perfeccionen sus habilidades de factorización. Si lo que busca son ecuaciones cuadráticas, vea entonces la próxima sección. Las hojas de ejercicios tienen diferentes niveles de dificultad, con las más sencillas al principio. Los coeficientes "a" que se mecionan son los de la expresión cuadrática general: ax2 + bx + c.
Factorizar Expresiones Cuadráticas

Ya sea que utilice el método de prueba y error, o la fórmula general de las ecuaciones cuadráticas, estas hojas de ejercicios incluyen muchísimas preguntas de práctica con sus respuestas. En la primera sección, las preguntas implican hallar las respuestas cuando las ecuaciones son iguales a cero, mientras que en la segunda, las ecuaciones son iguales a un número entero diferentes de cero.
Resolver Ecuaciones Cuadráticas Iguales a Cero (ax2 + bx + c = 0)

Resolver Ecuaciones Cuadráticas Iguales a Un Número Entero (ax2 + bx + c = d)
Otras Ecuaciones y Expresiones Polinomiales
Factorizar expresiones no cudráticas de diferentes niveles de complejidad.
Simplificar Polinomios que Incluyen Adición y Sustracción

Simplificar Polinomios que Incluyen Multiplicación y División

Simplificar Polinomios que Incluyen Todas las Operaciones

Factorizar Expresiones que No Incluyen Variables al Cuadrado
Factorizar Expresiones que Siempre Incluyen Variables al Cuadrado

Factorizar Expresiones que A Veces Incluyen Variables al Cuadrado

Multiplicar Polinomios con Dos Factores
Multiplicar Polinomios con Tres Factores
Inecuaciones
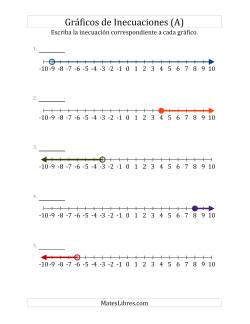
Ejercicios de inecuaciones que incluyen escribir la inecuación correspondiente a un gráfico, y graficar inecuaciones en una recta numérica.
Escribir la Inecuación Correspondiente a un Gráfico